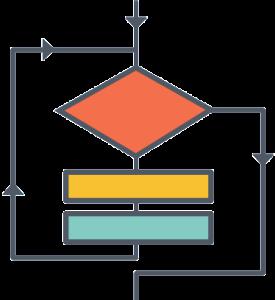
Grundtyper og eksempel på cykliske algoritmer

Artikel til formål at give en grundlæggende forståelse af, hvad en round robin, som er fælles for alle programmeringssprog og programmør uddannelse niveau.

Konceptet med en algoritme

En algoritme er en række handlingerat løse et beregningsmæssigt og andet problem i et begrænset antal trin. Handlinger (instruktioner) til udførelse af algoritmen kan udføres ene efter hinanden (sekventielt), samtidigt (parallelt) eller i vilkårlig rækkefølge, ved brug af cykler og overgangsvilkår. Algoritmer anvendes ikke kun i programmering, men også i andre aktivitetsområder, f.eks. I ledelsen af ​​produktions- og forretningsprocesser.

Cykliske algoritmer

En algoritme siges at være cyklisk, hvis den er i denDer er handlinger eller sæt af handlinger, der skal udføres mere end én gang. Gentagne algoritmiske handlinger er kroppens cyklus. Derudover har hver cyklus en betingelse om, at udførelsen af ​​den cykliske algoritme slutter.

Typer af cykliske algoritmer

Hver cyklisk algoritme har i sin sammensætningtilstanden af ​​sløjfen, det vil sige et logisk udtryk, hvis resultat bestemmer om sløjfekroppen vil blive udført igen eller sløjfen vil blive opsagt. Ved behandlingsmetoden er alle cykliske algoritmer opdelt i tre grupper.

Cyklus med forudsætning

I sådanne cykliske algoritmer kontrolleres kontinuitetsbetingelsen før behandling af sløjfekroppen, det vil sige, at der er behov for at gentage sløjfebehandlingen.

Overvej udgangen af ​​tal fra -5 til 0 som et eksempel på cykliske algoritmer med en forudsætning:

Algoritmens elementer:

1. Indstil startværdien af ​​basisvariablen j til -5.
2. Vi kontrollerer cyklusens tilstand. Tilstanden er positiv, og loopkroppen udføres for første gang.
3. Så tilføjer vi 1 til variablen j, vi kontrollerer igen cyklusens tilstand.
4. Sløjfen fortsætter med at løbe så længe værdien af ​​j er mindre end eller lig med nul, ellers forlader vi sløjfen på den falske gren

Cykle med postcondition

Tilstandskontrollen udføres efter den første behandling af sløjfekroppen og styrer udgangen fra den.

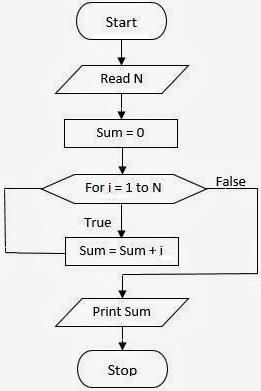
Lad os analysere beregningen af ​​summen fra 1 til tallet n som et eksempel på cykliske algoritmer, hvor postconditionen anvendes:

1. Vi indtaster et begrænset antal af beregningen af ​​summen n og angiver nul startværdier af summen summen og cyklens tæller i.
2. Sløjfen udføres før den første tilstandskontrol.
3. Vi kontrollerer tilstanden af ​​sløjfen, dvs. værdien af ​​tælleren i er mindre end eller lig med n.
4. Hvis resultatet af tilstanden er positivt, udfører vi sløjfen igen, ellers slutter vi sløjfen og udskriver summen på displayet eller udskrives.

Ubetinget cyklus

Det bruges normalt i algoritmer, når det krævede antal løbehjul er kendt på forhånd, og bruges meget ofte, når man arbejder med arrays.

En sådan algoritme indeholder tre obligatoriske elementer:

1. Startværdien, som kaldes loop-parameteren, fordi denne variabel ændres efter hver udførelse af cyklussen og bestemmer tidspunktet for dens gennemførelse.
2. Den værdi, som sløjfen slutter.
3. Trin cyklus.

Ved hvert trin verificerer programmet detOm startværdien er endelig. Og hvis ja, slutter cyklen. Ellers tilføjer vi trinstørrelsen til startværdien og cyklus gentagelserne. Det skal specielt bemærkes, at en ubetinget cyklus kan erstattes af en betinget med præ- eller postkondition.

Ved sammenlægning af cykliske algoritmer,overholder to obligatoriske betingelser. Først for at afslutte sløjfen er det nødvendigt, at kroppens indhold påvirker posten eller forudsætningen, ellers kan vi ende med en uendelig sløjfe. Men for nogle softwareopgaver anvendes sådanne cyklusser. Som et eksempel på cykliske algoritmer, der kører ubestemt, kan vi citere Windows-operativsystemet, hvor en uendelig musevælgercyklus bruges til at bestemme brugerens handlinger. For det andet skal variablerne, der sendes til sløjfen, tilvejebringe mindst en udførelse.

Beregning af factorial

For at konsolidere læsningen giver vi et eksempelcykliske algoritmer til beregning af faktoren af ​​et heltal. Ovennævnte eksempel er en loop med en forudsætning, men det er muligt at implementere enhver form for cyklisk algoritme.

• Input: data er et helt tal, for hvilket den factorial er defineret.
• Systemvariabler: parameteren for cyklen i, som tager værdier fra 1 til data i trin 1.
• Resultat: factorial variabel - faktorielle data, som er produktet af heltal fra 1 til data.

Overvej algoritmen i trin:

1. Algoritmen modtog nummerdataene, for hvilke det er nødvendigt at beregne det faktorielle.
2. Den variable faktor, hvor det endelige resultat bliver gemt, er tildelt en værdi på en.
3. Vi organiserer sløjfen med parameteren i og startværdien 1. Den endelige værdi er de oprindelige taldata. Når værdien af ​​tælleren i er større, slutter sløjfen.
4. Faktorisk beregningscyklus udføres - de nuværende værdier for faktorial og counter i multipliceres.
5. Til værdien af ​​tælleren tilføj en enhed, kontroller sløjfens tilstand, og hvis resultatet er positivt, afslutter vi det.
6. Efter den sidste iteration af løkken, værdien af ​​de faktorielle data! forbliver i factorial og vises eller udskrives.
</ ol </ p>